Nomos Alpha of Iannis XENAKIS for cello solo : guide for performers [NOMOS ALPHA of Iannis XENAKIS for cello solo: guide for performers

Name: Josquin Buvat Main subject: Cello Supervisor: Patrick van Deurzen Master circle leader: Martin Prchal Title: Nomos Alpha of Iannis Xenakis: guide for performers Research question: how build one's interpretation of Nomos Alpha ? And practice it? Summary of result: Today, Nomos Alpha (1965-66) is greeted with loud applause each time it is performed. And the piece is considered one of the greatest pieces of the 20th century's cello solo repertoire, still it's also one of most difficult and “avant-gardiste”. Furthermore, the piece remains 'Difficult' for the listener: it is submerged in the torrent of 144 micro-events, an extreme fragmentation accentuated by the presence of many silences. That's why Nomos is only rarely played. Since the piece's creation in 1966, lot of cellists were aware of the existence of Nomos Alpha. Many cellists had the score, but hardly anyone played it. It seemed important to me to begin my research with an analysis of the piece and an explanation of the historical musical context of that time. Indeed, Nomos alpha is one of Xenakis’s most ‘formalised’ pieces, the structure and all the parameters are calculated down to the last details. For cellists, these knowledges are essential to understanding the piece and making the necessary choices to build its interpretation of Nomos Alpha. In last the last part of this research, I have maked a guide for performers for the cellist who would like to play Nomos Alpha. For this guide I will try to concentrate on some essentials aspects of the piece for the performers. To illustrate this guide I did an critic comparative analysis of the different versions of the piece. And finally to complete this guide I did some videos of tutorials on how to practice the piece. Biography After completing his studies at Pôle Supérieur Paris Boulogne-Billancourt in Michel Strauss's cello class, as well as his Bachelor's degree in Musicology at Paris-Sorbonne University, Josquin Buvat continued his studies in a Master's degree in Performance at the Koninklijk Conservatorium Den Haag. Josquin gives a special place to modern music and contemporary creation in his repertoire. Since 2017, he has been a member of the Nomos ensemble, with which he has appeared at several festivals, including the Presences festival at Radio France, a concert that will be recorded. He performs regularly in chamber music as well as in orchestra, with Les Siècles, Ensemble Appasionato, Ensemble A-letheia the OJIF, the JOEHB. In addition to his musical activities Josquin is also involved in the field of associations, for two years including one as President of the Students Office of the PSPBB.

The organisation of the basic sounds: the group theory

Source:Fernand Vandenbogaerde,
analysis of Nomos Alpha of I.Xenakis

I-/ The groups of transformations

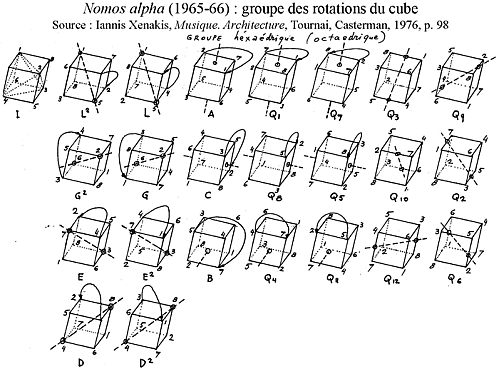
In the previous chapter I explained about the two different paths (A and B) Xenakis is using within each of the six parts. The basic sounds in Path A of Nomos Alpha are organized with the cube transformation onto itself in space.

There are 24 cube transformations in the space. The apexes of the cube are numbered from 1 to 8 (corresponding to basic sounds) and forms 2 tetrahedrons: 1 2 3 4 and 5 6 7 8. Each transformation gives a different permutation of the eight first numbers.
In the tables below, the 24 cube transformations:

We notice two groups of transformations.

- The group A: start with the first tetrahedrons 1 2 3 4, for example the transformation D: 2 3 1 4– 6 7 5 8

- The group Q: start with the second tetrahedrons 5 6 7 8, for exemple the transformation Q_1:7 8 6 5 – 3 4 2 1_.

In the group A there are 12 transformations: A, B, C, D, D², E, E², G, G², I, L and L^2.

In the group Q there are 12 transformations: Q₁, Q₂, Q₃, Q₄, Q₅, Q₆, Q₇, Q₈, Q₉, Q₁₀, Q₁₁and Q₁₂.

VI-/ The organisation of the lenghts, densities and intensities

These three parameters are organized with same concept as the basic sounds, with the cube transformations.

there are 4 different intensities: mf, f, ff and fff.
there are 8 different lenghts in second: 1-2.25-2.83-3.72-7.98-10-22.5

These parameters are grouped and like the basic sounds they are organized on each cube apexes like this:

IV-/ Last step from the subsets to the transformations

For the first section of Nomos Alpha, Xenakis choose in the subset V2 the transformation D, and for the second the transformation Q12 in the subset V4.

Reminder: the first product of the graph was V₂.V₄=V₆D є V₂ and Q₁₂∊ V₄

so we have D.Q₁₂ = Q_{4 and} Q₄∊V₆

and so on...

Also we find sequence of the transformation for the organisation of the basic sounds:

we can see clearly the repetitions of the chain V₂, V₄, V₆, V₃, V₅, V₆.

The sequences of the transformations are organized by the product of the transformations as in the table below.

II-/ The subsets

In each group there are 3 subset:

in A we have: V₁ = {I, A, B, C}, V₂ = {D, E²,G, L²} and V₃ = { D², E, G², L}.
in Q we have: V₄ = {Q₆, Q_12,Q₇, Q₁}, V₅ = {Q₈, Q₁₀, Q₃, Q₅} and V₆ = {Q₂, Q₄, Q₁₁Q₉,}

With the same reasoning as in Tables 1, we get the following table.

V-/ Analysis of the first two sections of Nomos Alpha

As we can see on the score beside, for the first section of Nomos Alpha Xenakis uses the transformation D, the sequence will be: 2 3 1 4 - 6 7 5 8. Consequently the order of the basic sounds in the first section should be:

III-/ The organisation of the basic sounds

Graphs and chains, how do they works ?

Example with the graph builting from V₂ and V₄ . this is the graph used for organizing the basic sounds.

First product V₂.V₄ = V₆ (result obtained with table 2)

The next product is the second factor and the result of the previous product, here the next product will be V₄.V₆.

Therefore here is the totality of the graph:

V₂.V₄=V₆ V₄.V₆=V3 V₆.V₃=V₅ V₃.V₅=V₆ V₅.V₆=V₂ V₆.V₂=V₄ V₂.V₄=V₆

At the end we have found the same product (V₂.V₄=V₆), so the cycle is over. Thus we get the chain: V₂, V₄, V₆, V₃, V₅, V₆.

As we can see in the form table of the piece there are 18 sections in the Path A, also this chain will be repeated 3 times. In this regard, each subset (V1, V2...V6) contains 4 transformations. Example: V₂ = {D, E²,G, L²}

Therefore, in each repetition of the chain, Xenakis will chooses a different transformation in each subset.

From this table, it is possible to make several graphs. A graph is a set of products, where here a product of the subsets V1, V2...V6. This process creates a chain of products, and gives Xenakis the sequence of cube transformations. In Nomos Alpha, Xenakis uses the graph building from V2 and V4 for the basic sounds organisation, and the graph building from V3 and V5 for the lengths, densities and intensities.

The second section uses the transformation Q12, also the sequence will be: 5 6 8 7- 1 2 4 3, Consequently the order of the basic sounds in the first section should be:

After this analysis, we are going to look at several questions about the perforamnce of the piece in the next part: Guide for performers

group A

group Q

group A

Group transformations of a cube

group Q

Table abstract to : Fernand Vandenbogaerde,
analysis of Nomos Alpha of I.Xenakis1

Table 1

Tables abstract to : Fernand Vandenbogaerde,
analysis of Nomos Alpha of I.Xenakis2

Table abstract to : Fernand Vandenbogaerde,
analysis of Nomos Alpha of I.Xenakis3

Observation: We notice that the transformations of the group A change the first tetrahedron (group A) in itself and the second (group Q) in itself (example 1).

On the contrary, the transformations of the Q group change the first tetrahedron in the second and conversely (example2).

Table 2

it's the same sequence we observed in the score in the previous part

Example 1:

A.A= A and A.Q=Q

That means, when the first term of the product is A the result of the product will be the second term.

Example 2:

Q.A= Q and Q.Q=A

That means, when the first term of the product is Q the result of the product will be the opposite of the second term..

Group A

Group Q

Table abstract to : Fernand Vandenbogaerde,
analysis of Nomos Alpha of I.Xenakis4

The 18 sections of the Path A

indication of the cube-transformation, for the first section. Here is the transformation D

Form table of Nomos Alpha

in the product Q.A
Q is the first term, and A the second.

reading guide of the table: reading direction.

Example with the Q.A=Q

second term

first term

Tip

Tip