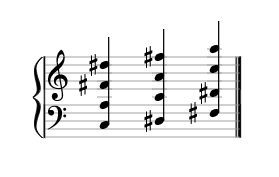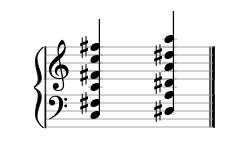Fractal of Periodic Musical Elements
a re-taxonomy of music for machine learning
Cognitive scientists like Shepard16, Deutsch17, and Burns18 conducted studies on the nature of the phenomenon of audible pitch circularity and octaves equivalence. It is beside the scope of this paper to investigate pitch circularity and octaves-equivalence as a psycho-acoustic phenomenon in relation to the new theory but could be considered interesting for further research. According to Dunne and McConnell19 circularities of pitch are not possible in just intonation tuning, because adding the fractional intervals of just intonation (in an exponential system multiplying their frequencies by each other) by other intervals smaller than an octave, can never exactly reach the octave back again. Douglas Hofstadter called any hierarchical systems coming back to their own beginning “strange loops”, and Shepard tones and musical scales special cases of them.20 In the context of Periodic Musical Elements, both periodic and aperiodic musical progressions can be analyzed with a set of modified Periodic Musical Elements, which I further explain in the next paragraph.
Some of the elements generated with skipping will miss samples of the original element. These elements have their fixed amount of transpositions that use the remaining frequencies until all frequencies from the original element are used. For instance, Skip 3 of equal temperament = 12 with sampling rate = 12 with root note = C3 generates an array of 4 melodic repetitions of an augmented chord: [ C3, E3, G#3, C3, E3, G#3, C3, E3, G#3, C3, E3, G#3 ]. Since there are 4 augmented chords possible to be created with notes of a chromatic scale, skip 3 of sampling rate 12 has 4 transpositions.
Modifiable parameters
The primary goal of the taxonomy is to enable the analysis of music with periodic elements. It would not be possible with only raising Shepard-tone-like progressions - to reach this possibility, I introduce four parameters for their modification: skip, transposition, rotation, and context.
Shepard tones are by definition increasing or decreasing, but a Shepard tone built only with tritones is increasing and decreasing at the same time.
In general, PMEs are periodic and hence they will contain the same progression of notes whenever they are started. However, when superimposing two or more elements with each other, it becomes crucial to specify which exact samples should be superimposed. This is why another needed parameter is rotation. It specifies from which sample the periodic progression is started.
Fractal of Periodic Musical Elements
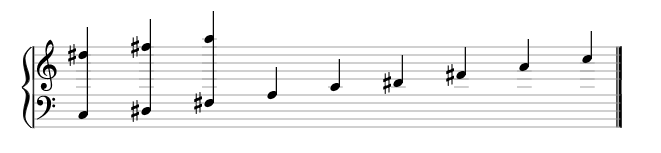
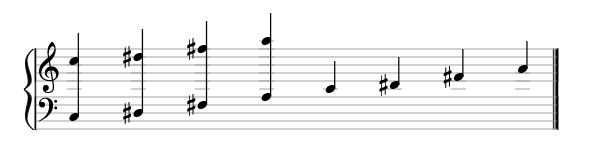
In 1964, Roger Shepard, a cognitive scientist at Stanford University, presented a Shepard tone as an aural illusion of infinitely raising or decreasing pitch.13 To create the illusion, the scientist spread equally-tempered scale pitches in octave relations above and below the original tones and gradually changed the dynamics of each note in the created progression. Later, Edward M. Burns presented evidence that the tones do not have to be spread by octaves for the illusion to be perceived.14 In my music compositions, I created Shepard tones based on multiple intervals simultaneously, for instance, based on a Tristan chord:
Considering that after the last chord of periodic progression music comes back to its own beginning, a Shepard tone built on a Tristan chord can be created by superimposing four rotations of a Shepard tone based on only one interval, achieved by adding the intervallic relations of its components. What is especially interesting here, is that it does not matter if the Shepard tone is rotated on an x-axis or on a y-axis (fig. 5). Observation of this phenomenon with different chords led me to an expectation that maybe any music harmony could be analysed with Shepard tones.
(Sampling rate 15):[ C, C#, D, D#, E, F, F#, G, G#, A, A#, B, null, null, null ],
(Sampling rate 14):[ C, C#, D, D#, E, F, F#, G, G#, A, A#, B, null, null ],
(Sampling rate 13):[ C, C#, D, D#, E, F, F#, G, G#, A, A#, B, null ],
Sampling rate 12: [ C, C#, D, D#, E, F, F#, G, G#, A, A#, B ], <- 12 TET as a melody
Sampling rate 11: [ [ C, B ], C#, D, D#, E, F, F#, G, G#, A, A# ],
Sampling rate 10: [ [ C, A# ], [ C#, B ] , D, D#, E, F, F#, G, G#, A ],
Sampling rate 9: [ [ C, A ], [ C#, A# ] , [ D, B ], D#, E, F, F#, G, G# ],
Sampling rate 8: [ [ C, G# ], [ C#, A ] , [ D, A# ], [ D#, B ], E, F, F#, G ],
Sampling rate 7: [ [ C, G ], [ C#, G# ] , [ D, A ], [ D#, A# ], [ E, B ], F, F# ],
Sampling rate 6: [ [ C, F# ], [ C#, G ] , [ D, G# ], [ D#, A ], [ E, A# ], [ F, B] ], <- 6 tritones
Sampling rate 5: [ [ C, F, A# ], [ C#, F#, B ], [ D, G ], [ D#, G# ], [ E, A] ],
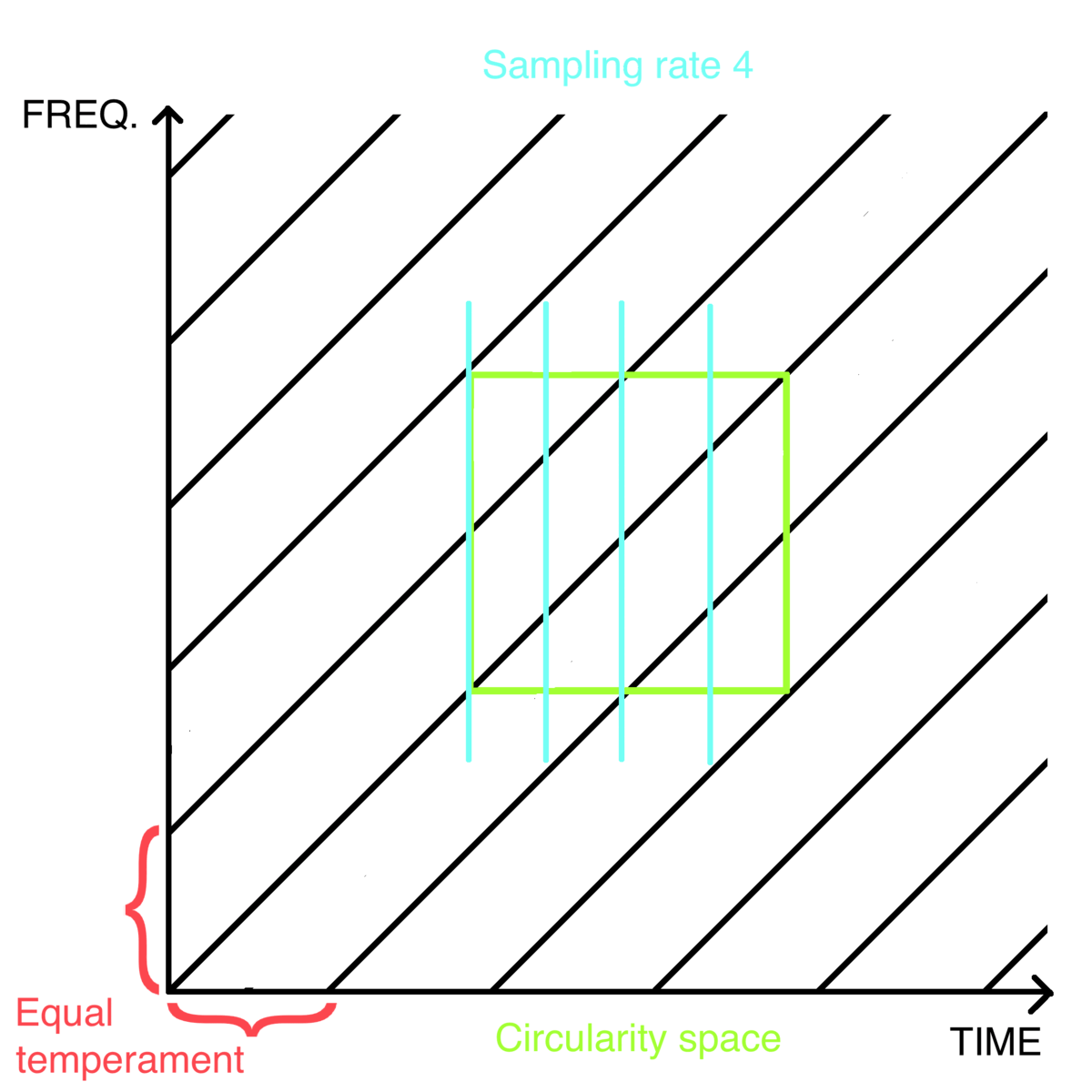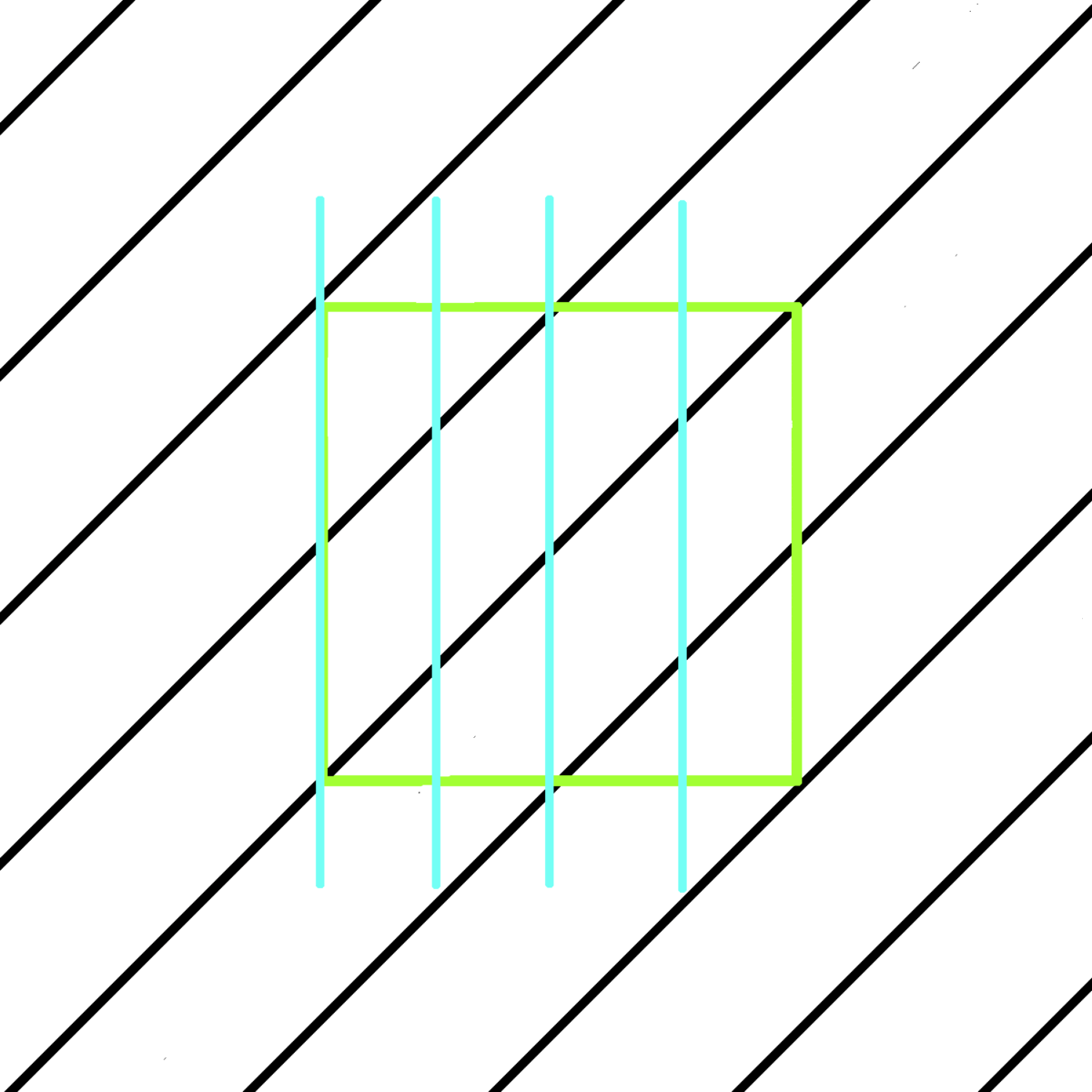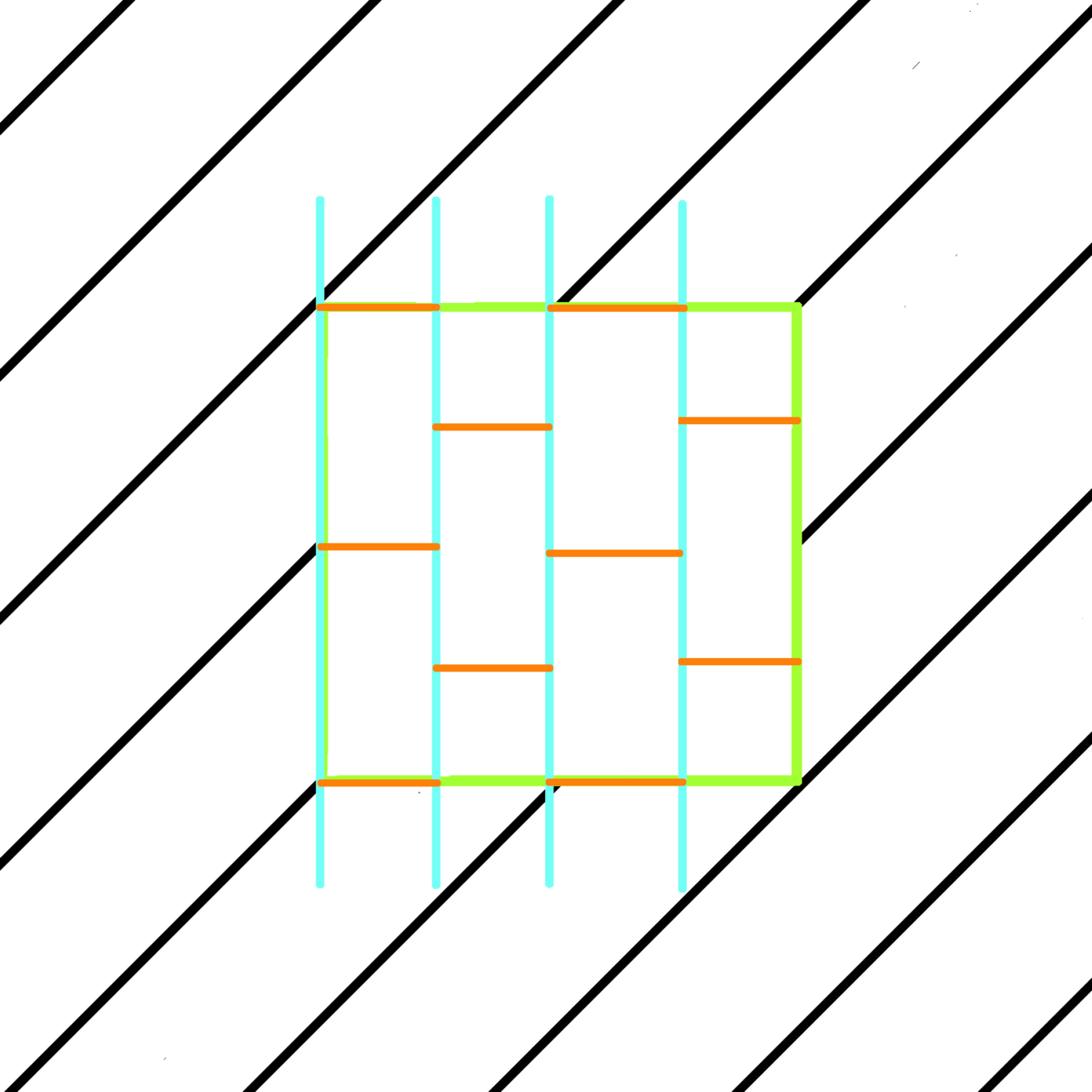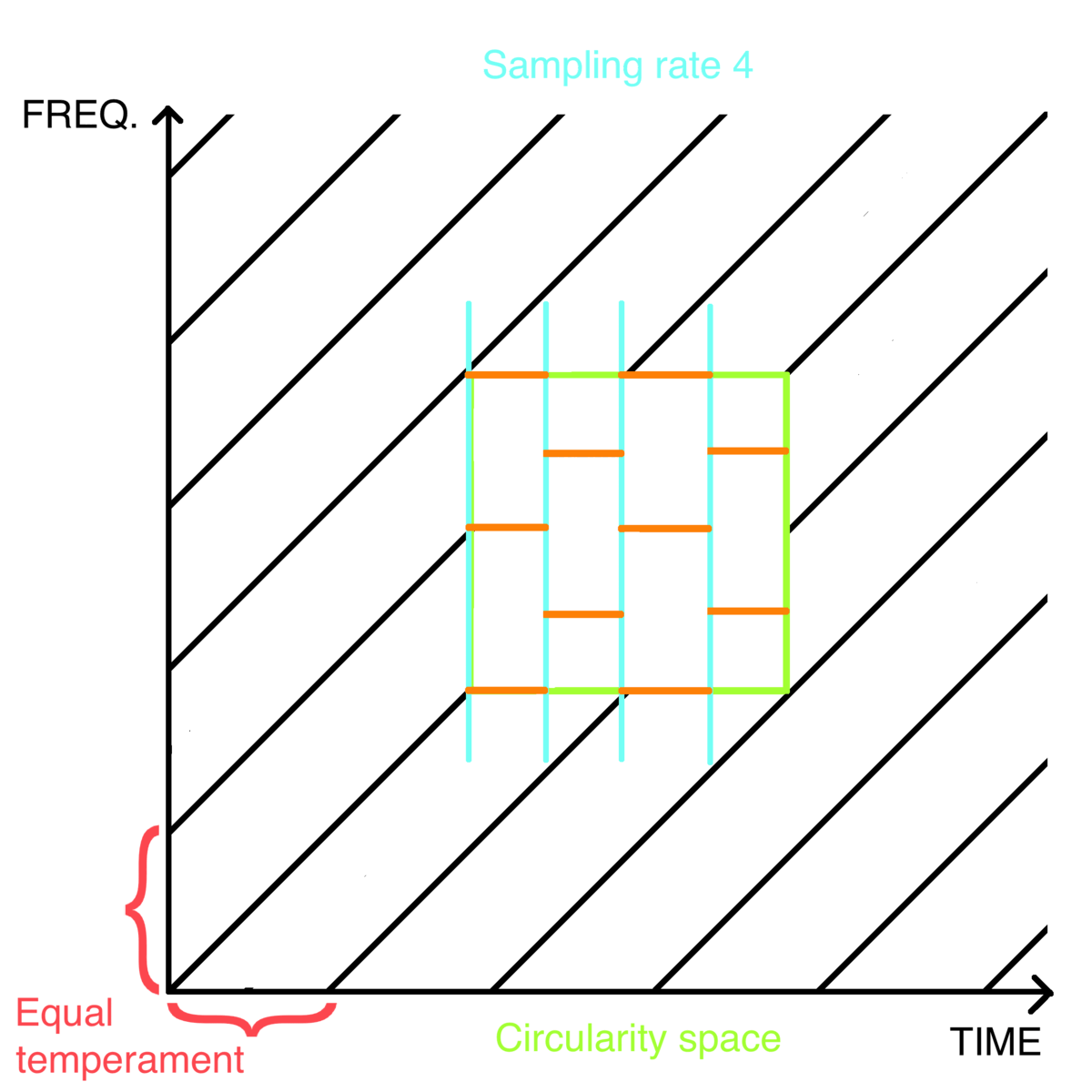
Sampling rate 4: [ [ C, E, G# ], [ C#, F, A ], [ D, F#, A# ], [ D#, G, B ] ], <- four aug chords
Sampling rate 3: [ [ C, D#, F#, A ], [ C#, E, G, A# ], [ D, F, G#, B ] ], <- three dim7 chords
Sampling rate 2: [ [ C, D, E, F#, G#, A# ], [ C#, D#, F, G, A, B ]], <- two whole-tone scales
Sampling rate 1: [ [ C, C#, D, D#, E, F, F#, G, G#, A, A#, B ] ], <- 12 TET as 1 chord
In these music examples, new pitches are introduced in intervallic relations of a Tritone, Major 3rd, and Perfect 4th. Horizontal melodic lines are dependent on the vertical intervals, thus new raising scales have to be introduced in similar time relations:
Inspired by the circular properties of Shepard-tones, I created a map of possible unique periodic harmonic progressions based on one interval, that can be used to synthesize more complicated progressions by superimposing their rotations with each other. I call these progressions Periodic Musical Elements (PMEs). PME, similarly to a Shepard tone has a fixed amount of samples (chords) and its material is gradually looped through these samples back to its beginning. The difference is that PME has only one level of dynamics and does not create an auditory illusion such as Shepard tones. PME is notated with previously presented time-independent notation. When superimposing PMEs with each other, the rules of the time-independent notation apply, thus any progression of harmony, rhythm, and dynamics (including Shepard tones themselves) can be obtained.
Making a scale periodic
To understand how notes can be distributed in PMEs, let's build an element with an equally tempered 12-tone scale and modify it to synthesize different musical progressions. In an exponential system (based on frequencies), consecutive steps x of any equally-tempered scale can be found by the following formula:
root frequency * (height ^ ( x / equal temperament) ),
where root frequency is the lowest frequency (x=0), height is a number by which the root frequency has to be multiplied to find the upper limit of an equally divided range (for instance 2 for an octave), x is a consecutive step of a scale ( x = 1,2,3,4 …etc ), and equal temperament is the number of notes in the scale. To create a chromatic scale on a pitch C3, a root frequency = 130.81 Hz, a height = 2 (for one octave), and an equal temperament = 12 are needed. Following the formula, 12 frequencies are obtained: [ 130.81, 138.59, 146.83, 155.56, 164.81, 174.61, 184.99, 195.99, 207.65, 220.00, 233.08, 246.94 ]. In an exponential function, a rule applies: exp(x+y)=exp x*exp y, which means that adding frequencies to each other is equal to multiplying the frequency by the powers used to get them, for instance, a result of 138.59/130.81 is the same as 155.56/146.83, because the interval distance between both of these pairs is a minor second.
In a linear system (based on integer numbers, for instance, midi notes), consecutive steps x of any equally-tempered scale can be found by the following formula:
root frequency + x * (equal temperament / height).
To create a chromatic scale on a midi note x0 = 60 (C3), a root frequency = 60, a height = 12 (for one octave), and an equal temperament = 12 are needed. Following the formula, 12 midi notes are obtained: [ 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71 ]. As mentioned earlier, associative arrays can be used to map any exponential scale onto a linear scale for easier calculations.
At least 12 samples are needed to notate the created array in a time-independent notation as a melody consisting of one note per sample. If the chosen sampling rate is smaller than the length of the created scale, it will continue to the next repeats of the element, thus the scale will wrap itself within the same periodic element. If the chosen sampling rate is higher than the number of notes in a scale, additional samples will be filled with a musical rest, in time-independent notation. This is also how pitches of any Shepard tone can be wrapped into periodic progression:
I created a parameter of skip to show all directions of a scale on a spectrum between increasing and decreasing. It changes the order of samples by looping through the samples of the element, skipping some of them until reaching the number of acquired samples equal to the sampling rate (fig. 8). For example, skip 5 of sampling rate 12 means that the algorithm should acquire only every fifth sample of the looped element until saving 12 samples in such modified order. The number of skips is always equal to the used sampling rate (or, further explained, sampling rate’s context).
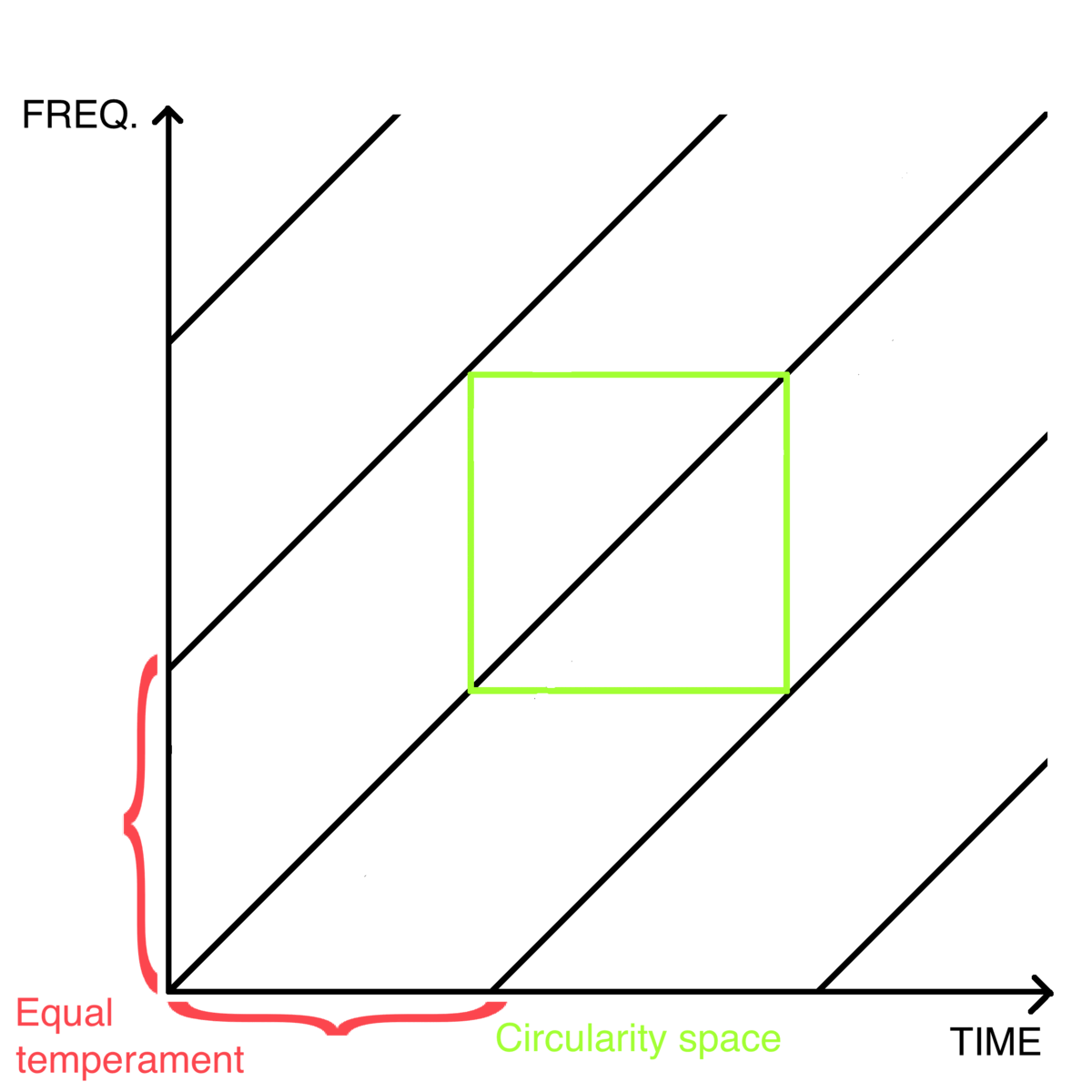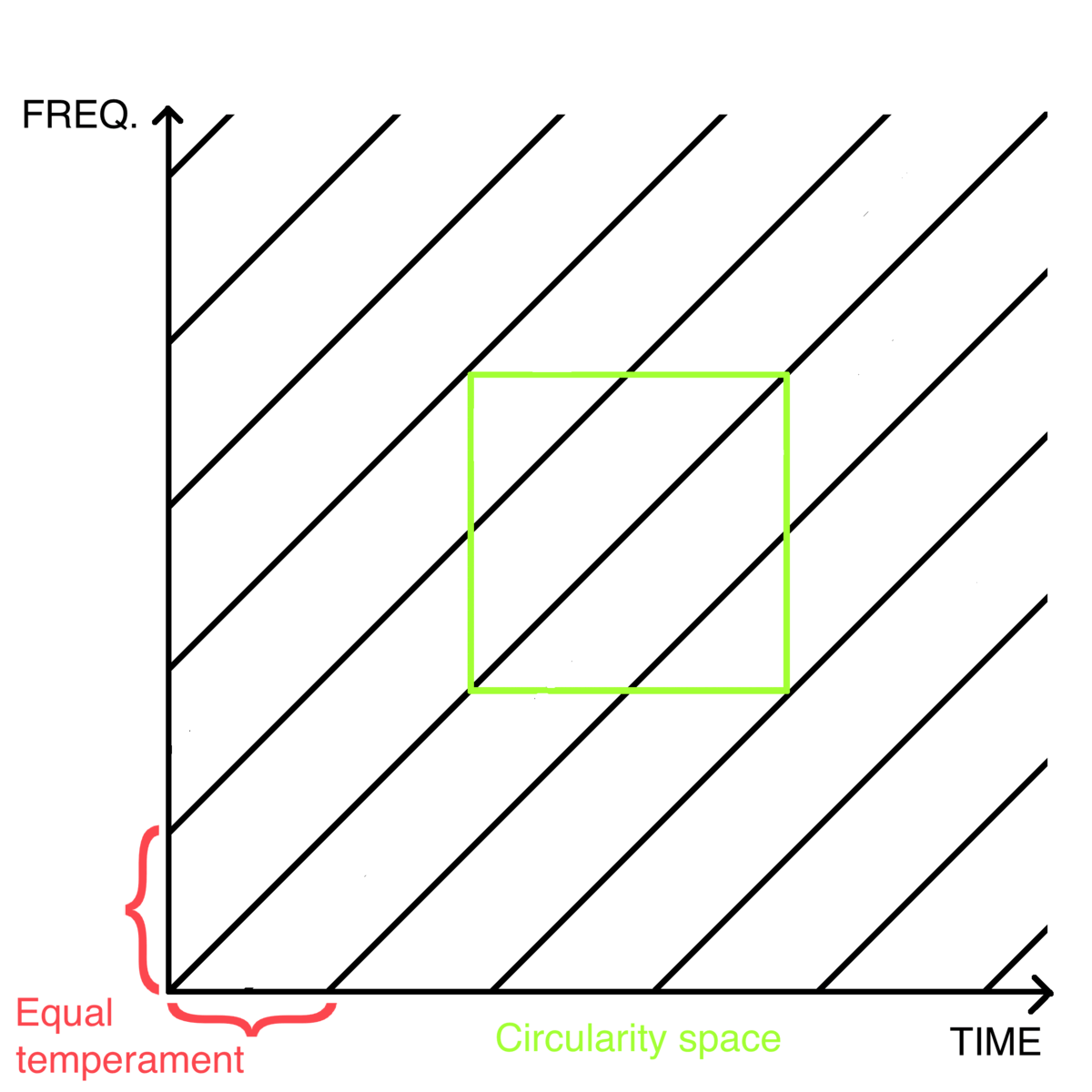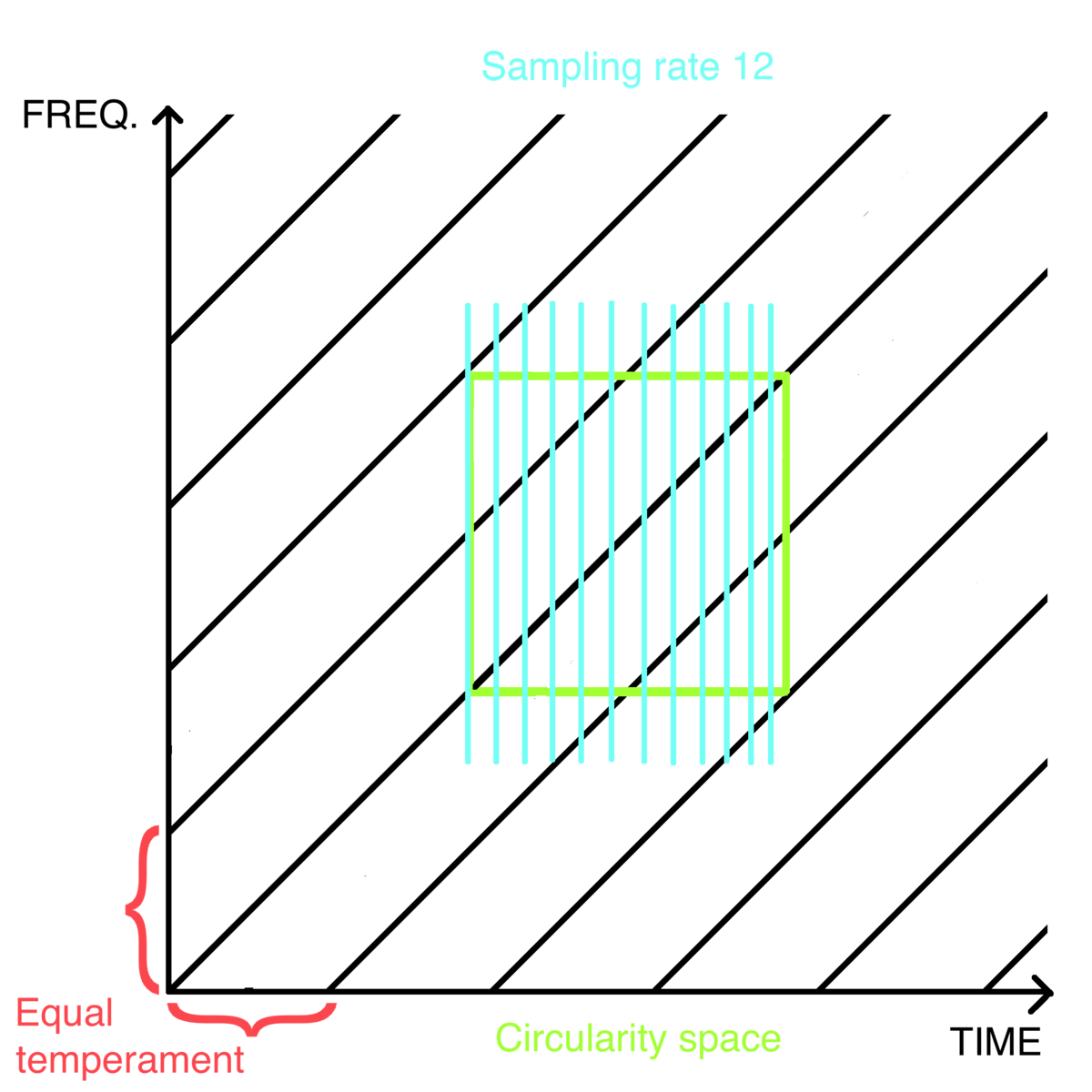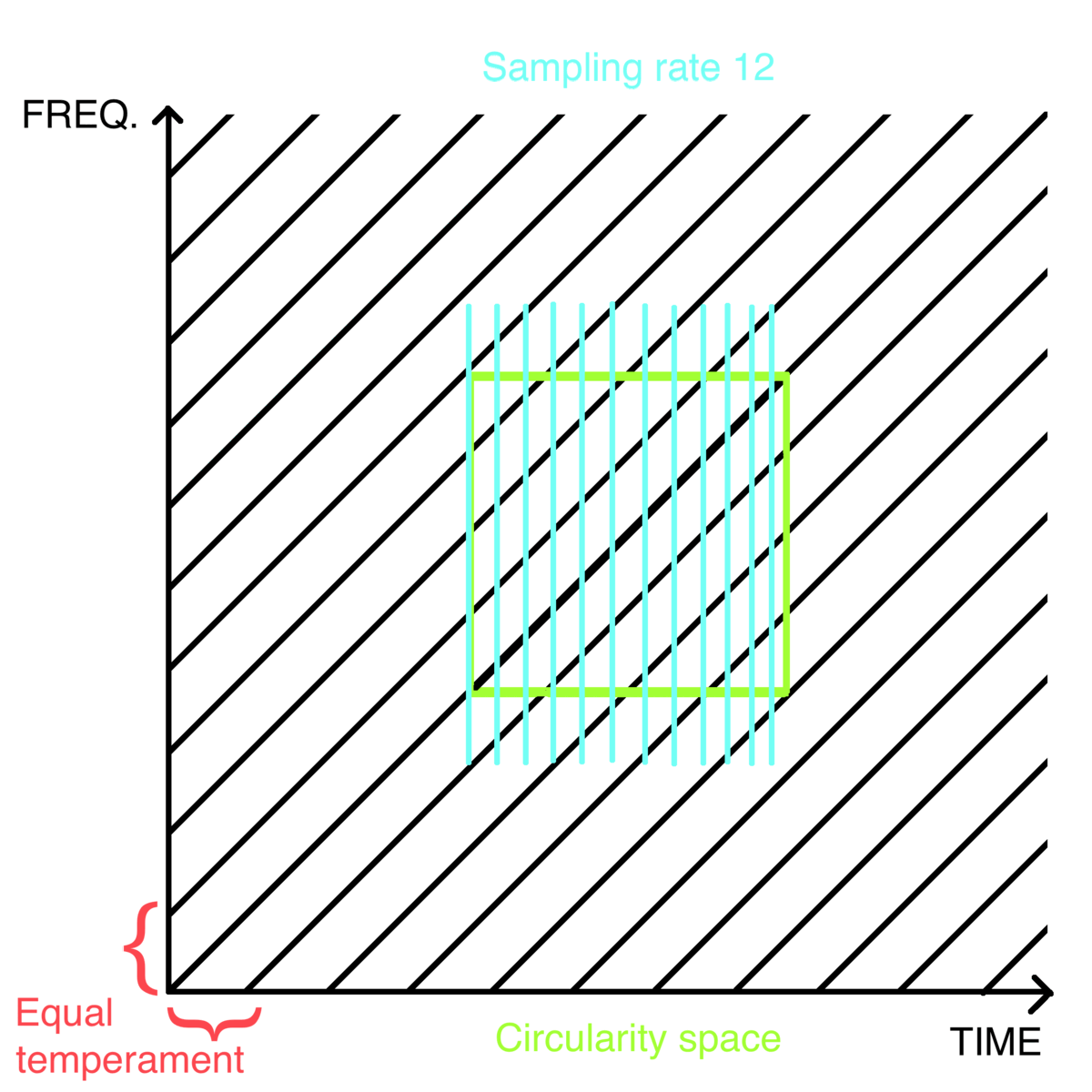
Periodic Musical Elements could be defined as musical progressions generated by sampling a Shepard-Risset glissando without dynamics, where equal temperament is a constant value determining the difference between the starting points of continuously-generated glissandi.
The paradox of pitch circularity
In 1968, French composer Jean Claude Risset created a version of a Shepard scale, called a Shepard-Risset glissando, in which steps between each tone of the scale are continuous glissandos.15
Amounts of transpositions and their rotations for any skip can be calculated in the following way:
For skips where: sampling rate % skip = 0:
- amount of transpositions = sampling rate / (sampling rate / skip),
- amount of rotations = sampling rate / skip
For skips where: skip > (sampling rate / 2) && sampling rate % (sampling rate - skip) = 0:
- amount of transpositions = sampling rate - skip,
- amount of rotations = sampling rate / (sampling rate % skip)
For other skips:
- skips have no transpositions because skipping will change the order of samples without missing any samples.
- each skip has a number of rotations equal to the sampling rate
Context of the sampling rate is a parameter that allows composing aperiodic elements with the use of Periodic Musical Elements by feeding samples with frequencies generated with a higher sampling rate than the one currently used for presenting the music material. For instance, a Periodic Musical Element can be created in a context of sampling rate 15 but presented in sampling rate 12. Such progression will be aperiodic because we will only see 12 first samples of the periodic element with a sampling rate of 15.
In object-oriented programming languages, a PME can be defined as an object with 4 attributes: skip, transposition, rotation, and context. Any musical progression written in previously presented time-independent notation can be analysed as a result of superimposing one or more such objects. Presented limits of possible modifications of Periodic Music Elements form an infinitely growing fractal, growing as more and more combinations of skips and their transpositions are presented for higher sampling rates (fig. 11). These limits create a system of musical limitations for a new taxonomy that I call a Fractal of Periodic Musical Elements. It can be used to synthesize and analyse music progressions of harmony, rhythm, and dynamics notated in a time-independent notation and can be used as a musical system for further investigations with supervised and unsupervised machine learning processes.
Fig. 4. Horizontal introductions of the scales are dependent on the vertical intervallic relations in chords
Fig. 5. Generating a Shepard tone with multiple intervals, by rotating a Shepard tone with one interval
Fig. 6. Text in time-independent notation and a slideshow (click the arrow to change slides) with music scores present a 12-tone equal temperament scale in 15 different sampling rates: