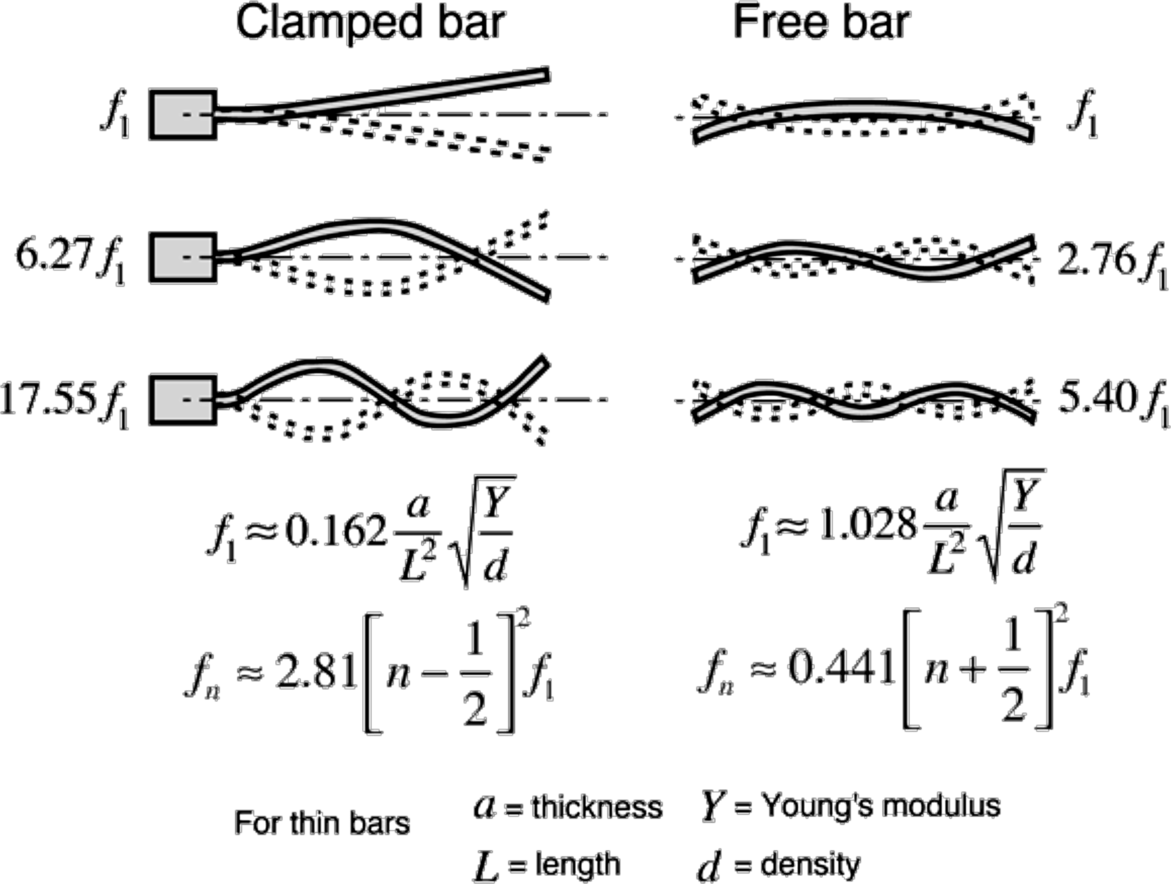
Figure 3. The elastic property involved in the vibration of bars is usually stated in terms of Young's Modulus. Bar Vibrational Modes
It is not intuitive to work with such configurations. Since density and elasticity of the material are relevant data, necessary for frequency calculations of vibrational modes, it can be hard for the common instrument builder, sound sculptor, or amateur explorer to predict the pitch of a clamped shape.30 This can be said for modelling any complex physical phenomena, but the non-harmonic behaviour of clamped shapes makes it even less intuitive. This is a significant reason that the Baschets relied on empirical trial and error methods, observing the results of various configurations of a specific material rather than attempting to calculate in advance.
Physics (formulas and calculations) can predict the first few partials for a clamped rod with regular prismatic geometry, but it is harder to predict the ratios of the partials above the third and fourth overtones. The difficulty of predicting higher partial ratios is even greater when the shape is not a uniform cylindrical rod. In most cases we are able to hear more than just the first few overtones, and so these calculations would be useful for predicting the resultant sound.
Our perception of all those overtones provides us with timbral information and provides a wide range of tonal perceptions (from clearly tonal to noise with no perceptible pitch), depending on the envelope of each overtone and the relationship of their frequencies.31
It is remarkable that many of the sound devices we have presented here feature lengths that create infrasonic frequencies (lower than 20Hz or close to the 50Hz but too weak to be heard), so the sounds we hear are actually only the higher overtones that appear in our hearing range. When we hear the upper partials without the fundamental, their ratios can be quite different than we would expect, resulting in unique timbres and distinctive cluster tones.32 That implies that a single rod can produce several kinds of sounds, not just high or low, but monodic, polyphonic, atonal, or “clustery,” depending on its length. Bart Hopkin demonstrates these phenomena with bright and accurate terms with his sliding rod, What a Shame, in this part of his lecture demonstration "Exploring the Science of Sound with Invented Musical Instruments."
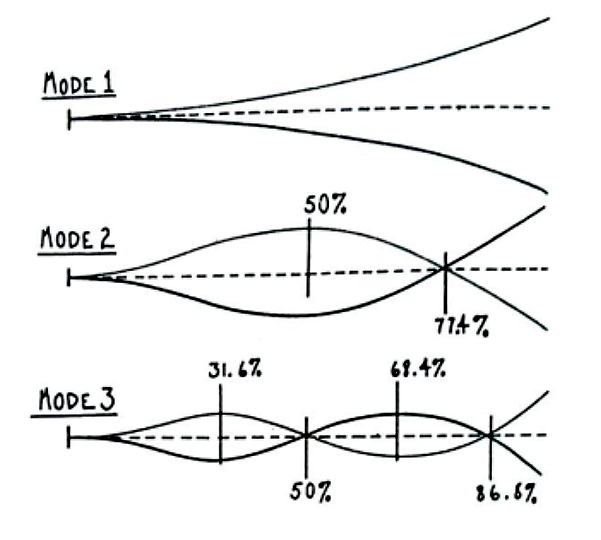
Figure 2. The first three modes of vibration for a rod fixed at one end. We can see that the nodal and antinodal points do not correspond to harmonic divisions in integer parts of the lengths. (Hopkin 1996: 40).
As shown in the image below, rods (or bars or plates) clamped on one end behave differently than freely-suspended rods. The node created at the clamping point creates new boundary conditions, which alter the tension and the vibrational behaviour of the rod.29
Vibrational Modes of Clamped Oscillators
Here we engage with the core aspectof our subject: a system of clamped oscillators will exhibit odd and non-intuitive vibrational modes when compared to harmonic oscillators (strings and air columns) that follow more predictable logic.26 For the purposes of this exposition, we are primarily referencing rods fixed at one end, although we will also use bars, plates, and other shapes as examples.27
A single rod clamped at one end (an inharmonic oscillator) does not behave according to the (well understood and accepted) harmonic vibrational patterns. A clamped element will produce a fundamental vibration and a set of partial overtones bearing no harmonic (simple integer) ratio to the fundamental. The overtones will correspond to the different shorter wavelengths that appear along the body of the oscillator depending on the geometry and internal tension of the element, externally imposed. Each partial will bear a complex mathematical relationship to the fundamental. The interval between each partial is highly variable, and it is typically not a simple integer multiple of the fundamental but an irrational number.28
Figure 4. Fragment of Bart Hopkin’s lecture Exploring the Science of Sound with Invented Musical Instruments
In his demonstration, we can hear the timbre changing radically depending on the order of overtones we hear. We can try to describe these variations in sound (with words such as resonant bell sounds, short and deep kalimba plucks, shallow ringing tones, etc.), and we can learn to identify these length configurations for use in our analysis of existing sound devices or new sound designs. All of these complex configurations, ratios of length to thickness to elasticity that affect ratios amongst overtones, appear in the Baschet pieces we have presented in this exposition. Variations of these configurations may produce a clear tone (in which one pitch is well-defined and clearly dominant), two or more tones (heard as clusters or chords with several identifiable pitches but no clearly dominant pitch), or an unclear tone sensation bearing only timbral information (too many pitches or none to be identified).
The goal of our discussion is to further the understanding of the complex relationships that exist in the vibrational patterns of clamped rods and the resultant sound qualities, based upon real examples. It is a complicated endeavor, but we can build up a sound library in our mind’s ear, in our sonic imagination, so we can build up an intuitive understanding of these phenomena and go deeper into sound sculpting with complex, inharmonic, and not – yet – common sounds.